Wikipedia
This text was copied from Wikipedia on 18 April 2024 at 3:10AM.
 | This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages)
|


| Computing devices in |
| Rabdology |
|---|
| Napier's bones |
| Promptuary |
| Location arithmetic |
Napier's bones is a manually-operated calculating device created by John Napier of Merchiston, Scotland for the calculation of products and quotients of numbers. The method was based on lattice multiplication, and also called rabdology, a word invented by Napier. Napier published his version in 1617.[1] It was printed in Edinburgh and dedicated to his patron Alexander Seton.
Using the multiplication tables embedded in the rods, multiplication can be reduced to addition operations and division to subtractions. Advanced use of the rods can extract square roots. Napier's bones are not the same as logarithms, with which Napier's name is also associated, but are based on dissected multiplication tables.
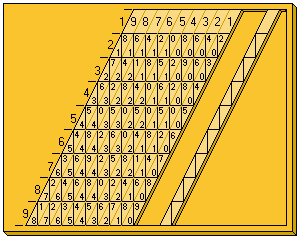
The complete device usually includes a base board with a rim; the user places Napier's rods and the rim to conduct multiplication or division. The board's left edge is divided into nine squares, holding the numbers 1 to 9. In Napier's original design, the rods are made of metal, wood or ivory and have a square cross-section. Each rod is engraved with a multiplication table on each of the four faces. In some later designs, the rods are flat and have two tables or only one engraved on them, and made of plastic or heavy cardboard. A set of such bones might be enclosed in a carrying case.
A rod's face is marked with nine squares. Each square except the top is divided into two halves by a diagonal line from the bottom left corner to the top right. The squares contain a simple multiplication table. The first holds a single digit, which Napier called the 'single'. The others hold the multiples of the single, namely twice the single, three times the single and so on up to the ninth square containing nine times the number in the top square. Single-digit numbers are written in the bottom right triangle leaving the other triangle blank, while double-digit numbers are written with a digit on either side of the diagonal.
If the tables are held on single-sided rods, 40 rods are needed in order to multiply 4-digit numbers – since numbers may have repeated digits, four copies of the multiplication table for each of the digits 0 to 9 are needed. If square rods are used, the 40 multiplication tables can be inscribed on 10 rods. Napier gave details of a scheme for arranging the tables so that no rod has two copies of the same table, enabling every possible four-digit number to be represented by 4 of the 10 rods. A set of 20 rods, consisting of two identical copies of Napier's 10 rods, allows calculation with numbers of up to eight digits, and a set of 30 rods can be used for 12-digit numbers.
Multiplication
The simplest sort of multiplication, a number with multiple digits by a number with a single digit, is done by placing rods representing the multi-digit number in the frame against the left edge. The answer is read off the row corresponding to the single-digit number which is marked on the left of the frame, with a small amount of addition required, as explained in the examples below.
When multiplying a multi-digit number by another multi-digit number, the larger number is set up on the rods in the frame. An intermediate result is produced by the device for multiplication by each of the digits of the smaller number. These are written down and the final result is calculated by pen and paper.
To demonstrate how to use Napier's bones for multiplication, three examples of increasing difficulty are explained below.
Multiplication by a small single-digit number
The first example computes 425 × 6.
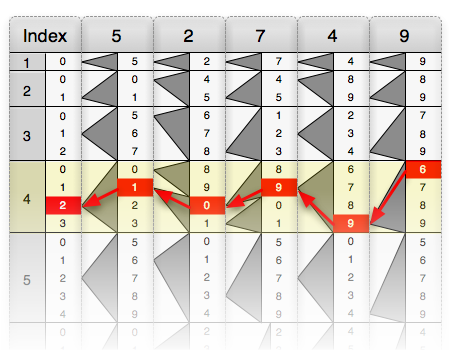
Napier's bones for 4, 2, and 5 are placed into the board, in sequence. These bones show the larger figure which will be multiplied. The numbers lower in each column, or bone, are the digits found by ordinary multiplication tables for the corresponding integer, positioned above and below a diagonal line. (For example, the digits shown in the seventh row of the 4 bone are 2⁄8, representing 7 × 4 = 28.) In the example below for 425 × 6, the bones are here depicted as red (4), yellow (2), and blue (5).

The left-most column, preceding the bones shown coloured, may represent the 1 bone. (A blank space or zero to the upper left of each digit, separated by a diagonal line, should be understood, since 1 × 1 = 01, 1 × 2 = 02, 1 x 3 = 03, etc.) A small number is chosen, usually 2 through 9, by which to multiply the large number. In this example the small number by which to multiply the larger is 6. The horizontal row in which this number stands is the only row needed to perform the remaining calculations and may now be viewed in isolation.

For the calculation, the digits separated by vertical lines (i.e. paired between diagonal lines, crossing over from one bone to the next) are added together to form the digits of the product. The final (right-most) number on that row will never require addition, as it is always isolated by the last diagonal line, and will always be the final digit of the product. In this example, there are four digits, since there are four groups of bone values lying between diagonal lines. The product's digits will stand in the order as calculated left to right. Apart from the first and the final digit, the product's digits will each be the sum of two values taken from two different bones.

Bone values are added together, as described above, to find the digits of the product. In this diagram, the third product digit from the yellow and blue bones have their relevant values coloured green. Each sum is written in the space below. The sequence of the summations from left to right produces the figure of 2550. Therefore, the solution to multiplying 425 by 6 is 2550.
Multiplication by a larger single-digit number
When multiplying by larger single digits, it is common that upon adding a diagonal column, the sum of the numbers results in a number that is 10 or greater.
The second example computes 6785 × 8.
Like Example 1, the corresponding bones to the biggest number are placed in the board. For this example, bones 6, 7, 8, and 5 were placed in the proper order as shown below.

In the first column, the number by which the biggest number is multiplied by is located. In this example, the number was 8. Only row 8 will be used for the remaining calculations, so the rest of the board has been cleared for clarity in explaining the remaining steps.

Just as before, each diagonal column is evaluated, starting at the right side. If the sum of a diagonal column equals 10 or greater, the "tens" place of this sum must be carried over and added along with the numbers in the adjacent left column as demonstrated below.

After each diagonal column is evaluated, the calculated numbers are read from left to right to produce a final answer; in this example, 54280 was produced.
Therefore: The solution to multiplying 6785 by 8 is 54280.
Multiplication by a multi-digit number
The third example computes 825 × 913.
The corresponding bones to the leading number are placed in the board. For this example, the bones 8, 2, and 5 were placed in the proper order as shown below.

To multiply by a multi-digit number, multiple rows are reviewed. For this example, the rows for 9, 1, and 3 have been removed from the board for clarity.

Each row is evaluated individually and each diagonal column is added as explained in the previous examples. The sums are read from left to right, producing the numbers needed for the long hand addition calculations to follow. For this example, row 9, row 1, and row 3 were evaluated separately to produce the results shown below.

Starting with the rightmost digit of the second number, the sums are placed from the rows in sequential order as seen from right to left under each other while utilising a 0 for a place holder.
2475 8250 742500
The rows and place holders are summed to produce a final answer.
2475
8250
+ 742500
753225
In this example, the final answer produced was 753225. Therefore: The solution to multiplying 825 by 913 is 753225.
Division
Division is performed in a similar fashion. To divide 46785399 by 96431, the bars for the divisor (96431) are placed on the board, as shown in the graphic below. Using the abacus, all the products of the divisor from 1 to 9 are found by reading the displayed numbers. Note that the dividend has eight digits, whereas the partial products (save for the first one) all have six. So the final two digits of 46785399, namely the '99', are temporarily ignored, leaving the number 467853. Then, the greatest partial product that is less than the truncated dividend is found. In this case, 385724. Two things must be marked down, as seen in the diagram: since 385724 is in the '4' row of the abacus, a '4' is marked down as the left-most digit of the quotient; the partial product, left-aligned, under the original dividend, is also written. The two terms are subtracted, which leaves 8212999. The same steps are repeated: the number is truncated to six digits, the partial product immediately less than the truncated number is chosen, the row number is written as the next digit of the quotient, and the partial product is subtracted from the difference found in the first repetition. The process is shown in the diagram. The cycle is repeated until the result of subtraction is less than the divisor. The number left is the remainder.

So in this example, what remains is a quotient of 485 with a remainder of 16364. The process usually stops here and the answer uses the fractional form 485+16364/96431.
For more accuracy, the cycle is continued to find as many decimal places required. A decimal point is marked after the last digit of the quotient and a zero is appended to the remainder which leaves 163640. The cycle is continued, each time appending a zero to the result after the subtraction.
Extracting square roots
For extracting the square root, an additional bone is used which is different from the others as it has three columns. The first column has the first nine square numbers, the second has the first nine even numbers, and the last has the numbers 1 to 9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | √ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0⁄1 | 0⁄2 | 0⁄3 | 0⁄4 | 0⁄5 | 0⁄6 | 0⁄7 | 0⁄8 | 0⁄9 | 0⁄1 2 1 |
| 2 | 0⁄2 | 0⁄4 | 0⁄6 | 0⁄8 | 1⁄0 | 1⁄2 | 1⁄4 | 1⁄6 | 1⁄8 | 0⁄4 4 2 |
| 3 | 0⁄3 | 0⁄6 | 0⁄9 | 1⁄2 | 1⁄5 | 1⁄8 | 2⁄1 | 2⁄4 | 2⁄7 | 0⁄9 6 3 |
| 4 | 0⁄4 | 0⁄8 | 1⁄2 | 1⁄6 | 2⁄0 | 2⁄4 | 2⁄8 | 3⁄2 | 3⁄6 | 1⁄6 8 4 |
| 5 | 0⁄5 | 1⁄0 | 1⁄5 | 2⁄0 | 2⁄5 | 3⁄0 | 3⁄5 | 4⁄0 | 4⁄5 | 2⁄5 10 5 |
| 6 | 0⁄6 | 1⁄2 | 1⁄8 | 2⁄4 | 3⁄0 | 3⁄6 | 4⁄2 | 4⁄8 | 5⁄4 | 3⁄6 12 6 |
| 7 | 0⁄7 | 1⁄4 | 2⁄1 | 2⁄8 | 3⁄5 | 4⁄2 | 4⁄9 | 5⁄6 | 6⁄3 | 4⁄9 14 7 |
| 8 | 0⁄8 | 1⁄6 | 2⁄4 | 3⁄2 | 4⁄0 | 4⁄8 | 5⁄6 | 6⁄4 | 7⁄2 | 6⁄4 16 8 |
| 9 | 0⁄9 | 1⁄8 | 2⁄7 | 3⁄6 | 4⁄5 | 5⁄4 | 6⁄3 | 7⁄2 | 8⁄1 | 8⁄1 18 9 |
To find the square root of 46785399, its digits are grouped into twos starting from the right so it looks like this:
- 46785399
- Note: A number with an odd number of digits like 85399 would be grouped as 085399
The leftmost group is chosen first, in this case 46. The largest square on the square root bone less than 46 is picked, which is 36 from the sixth row. The first digit of the solution is 6, since the sixth row was chosen.
Then, the number in the second column from the sixth row on the square root bone, 12, is set on the board.
The value in the first column of the sixth row, 36, is subtracted from 46, which leaves 10.
The next group of digits, 78, is added next to 10; this leaves the remainder 1078.
At this stage, the board and intermediate calculations should look like this:
|
√46 78 53 99 = 6
− 36
10 78
|
The numbers in each row are "read", ignoring the second and third columns from the square root bone; these are recorded. (For example, the sixth row is read as: 0⁄6 1⁄2 3⁄6 → 756).
Like in multiplication shown before, the numbers are read from right to left and add the diagonal numbers from top-right to left-bottom (6 + 0 = 6; 3 + 2 = 5; 1 + 6 = 7).
The largest number less than the current remainder, 1078 (from the eighth row), is found.
|
√46 78 53 99 = 68
− 36
10 78
− 10 24
54
|
Like before, 8 is appended to get the next digit of the square root and the value of the eighth row, 1024, is subtracted from the current remainder, 1078, to get 54. The second column of the eighth row on the square root bone, 16, is read and the number is set on the board as follows.
The current number on the board is 12. The first digit of 16 is added to 12, and the second digit of 16 is appended to the result. So the board should be set to:
- 12 + 1 = 13 → append 6 → 136
- Note: If the second column of the square root bone has only one digit, this is appended to the current number on the board.
The board and intermediate calculations now look like this.
|
√46 78 53 99 = 68
− 36
10 78
− 10 24
54 53
|
Once again, the row with the largest value less than the current partial remainder, 5453, is found. This time, it is the third row with 4089.
|
√46 78 53 99 = 683
− 36
10 78
− 10 24
54 53
− 40 89
13 64
|
The next digit of the square root is 3. The same steps as before are repeated and 4089 is subtracted from the current remainder, 5453, to get 1364 as the next remainder. When the board is rearranged, the second column of the square root bone is 6, a single digit. So 6 is appended to the current number on the board, 136, to leave 1366 on the board.
- 136 → append 6 → 1366
|
√46 78 53 99 = 683
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
|
The process is repeated again. Now, the largest value on the board smaller than the current remainder, 136499, is 123021 from the ninth row.
The value of every row often doesn't need to be found to get the answer. The row that has the answer may be guessed by looking at the number on the first few bones and comparing it with the first few digits of the remainder. But the diagrams show the value of all rows to make it understandable.
9 is appended to the result and 123021 is subtracted from the current remainder.
|
√46 78 53 99 = 6839
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
− 12 30 21
1 34 78
|
If all the digits have been used, and a remainder is left, then the integer part is solved, but a fractional bit still needs to be found.
If the integer part is solved, the current result squared (68392 = 46771921) must be the largest perfect square smaller than 46785899.
This idea is used later on to understand how the technique works, but more digits can be generated.
Similar to finding the fractional portion in long division, two zeros are appended to the remainder to get the new remainder 1347800. The second column of the ninth row of the square root bone is 18 and the current number on the board is 1366.
- 1366 + 1 → 1367 → append 8 → 13678
is computed to set 13678 on the board.
The board and intermediate computations now look like this.
|
√46 78 53 99.00 = 6839.
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
− 12 30 21
1 34 78 00
|
The ninth row with 1231101 is the largest value smaller than the remainder, so the first digit of the fractional part of the square root is 9.
|
√46 78 53 99.00 = 6839.9
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
− 12 30 21
1 34 78 00
− 1 23 11 01
11 66 99
|
The value of the ninth row is subtracted from the remainder and a few more zeros are appended to get the new remainder 11669900. The second column on the ninth row is 18 with 13678 on the board, so
- 13678 + 1 → 13679 → append 8 → 136798
is computed to set 136798 on the board.
|
√46 78 53 99.00 00 = 6839.9
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
− 12 30 21
1 34 78 00
− 1 23 11 01
11 66 99 00
|
The steps can be continued to find as many digits needed and if the precision needed is achieved. If the remainder becomes zero, this means the exact square root was found.
Rounding up
Having found the desired number of digits, it is easy to determine whether or not it needs rounding up; i.e., changing the last digit. Another digit doesn't need to be found to see if it is equal to or greater than 5. 25 is appended to the root and it is compared to the remainder; if it is less than or equal to the remainder, then the next digit will be at least five and rounding up is needed. In the example above, 6839925 is less than 11669900, so the root needs to be rounded up to 6840.0.
To find the square root of a number that isn't an integer, say 54782.917, everything is the same, except that the digits to the left and right of the decimal point are grouped into twos.
So 54782.917 would be grouped as
- 054782.9170
Then the square root can be found using the process previously mentioned.
Diagonal modification
During the 19th century, Napier's bones were transformed to make them easier to read. The rods were made with an angle of about 65° so that the triangles that had to be added were aligned. In this case, in each square of the rod the unit is to the right and the ten (or the zero) to the left.
The rods were made such that the vertical and horizontal lines were more visible than the line where the rods touched, making the two components of each digit of the result easier to read. Thus, in the picture it is immediately clear that:
- 987654321 × 5 = 4938271605
Genaille–Lucas rulers
In 1891, Henri Genaille invented a variant of Napier's bones which became known as Genaille–Lucas rulers. By representing the carry graphically, the results of simple multiplication problems can be read directly, with no intermediate mental calculations.
The following example calculates 52749 × 4 = 210996.
See also
References
- ^ John Napier (1617). Rabdologiæ (in Latin). Edinburgh, Scotland.
External links
 Media related to Napier's bones at Wikimedia Commons
Media related to Napier's bones at Wikimedia Commons- Wolfram Demonstration implementation of Napier bones in various number systems at cut-the-knot
- Napier and other bones and many calculators


1 Annotation
Second Reading
Terry Foreman • Link
John Napier's bones and other interests in maths were spurred by his desire to calculate the date of the Apocalypse.
"Napier had an interest in the Book of Revelation, from his student days at St Salvator's College, St Andrews. Under the influence of the sermons of Christopher Goodman, he developed a strongly anti-papal reading. He further used the Book of Revelation for chronography, to predict the Apocalypse, in A Plaine Discovery of the Whole Revelation of St. John (1593), which he regarded as his most important work; he also applied the Sibylline Oracles, to calculate the date of the end of the world. Napier believed that would occur in 1688 or 1700. He dated the seventh trumpet to 1541.
"In his dedication of the Plaine Discovery to James VI, dated 29 Jan 1594,[6] Napier urged the king to see "that justice be done against the enemies of God's church," and counselled the King "to reform the universal enormities of his country, and first to begin at his own house, family, and court." The volume includes nine pages of Napier's English verse. It met with success at home and abroad. In 1600 Michiel Panneel produced a Dutch translation, and this reached a second edition in 1607. In 1602 the work appeared at La Rochelle in a French version, by Georges Thomson, revised by Napier, and that also went through several editions (1603, 1605, and 1607). A new edition of the English original was called for in 1611, when it was revised and corrected by the author, and enlarged by the addition of A Resolution of certain Doubts proponed by well-affected brethren; this appeared simultaneously at Edinburgh and London." http://en.wikipedia.org/wiki/John…